University

UNIVERSITY PHYSICS

Classical Mechanics I - Term 1A

This course has the student review all concepts from Grade 11 and 12, usually up to the first half of its length. While doing so, it steps up the difficulty of problems, introducing twists in otherwise familiar settings. For instance, inclines might now be moveable, pulleys may have more than one connection to a mass, etc. Beyond the midterm stage, it teaches students to handle extended objects and the resulting motions thereof. Rigid bodies can now rotate, translate and even roll!

  1. Kinematics in 1D
    1. Predicting Motion
    2. Collision Setups
  2. Kinematics in 2D
    1. Projectile Motion
  3. Relative Motion
    1. Reference Frame Transformations
    2. Air, Water and Ground references
  4. Introduction to Forces
    1. Applied Forces
    2. Gravity
    3. Normal Force
    4. Tension
    5. Friction
    6. Fictitious Forces
  5. Force Problems
    1. Inclines
    2. Pulley Systems
    3. Slip Limit
    4. Circular Motion
    5. Accelerated Frames
  6. Energy
    1. Work done by a Force
    2. Types of Energy
    3. Energy Conservation
  7. Linear Momentum
    1. Momentum relation to force
    2. Conservation of momentum
    3. Types of Collisions
  8. Center of Mass (C.O.M)
    1. Finding the C.O.M
    2. Relating momentum conservation to C.O.M
  9. Angular Kinematics
  10. Angular Dynamics
    1. Moment of Inertia
    2. Torque
    3. Newton’s second law (Angular Form)
  11.  Angular Momentum
    1. Rotational Collisions
    2. Connection with C.O.M and Moment of Inertia
  12. Statics
  13. Rolling Motion

Classical Mechanics II - Term 1B

This type of course continues on mechanics by introducing position dependent forces (Spring, Electric etc.). Students learn to analyze periodic motion that includes pendulums and eventually waves. The framework of wave physics is set in place and students use it to later embark on their journey understanding phenomena in electricity and magnetism. Light becomes the derivative of the above discussions and occupies the rest of this course. Optical phenomena are explained and the quantum nature of light and the atom are also investigated.

  1. Simple Harmonic Motion (SHM)
    1. General Solution to SHM
    2. Finding phase
    3. Energy Conservation
    4. Springs In-Series/Parallel
  2. Pendulums
    1. Simple Pendulums
    2. Physical Pendulums
  3. Physical Wave Properties
    1. Frequency
    2. Wavelength
    3. Period
  4. Traveling Waves
    1. Equation of Motion
    2. Wave speed vs Oscillation speed
  5. Wave Interference
    1. Constructive/Destructive Interference
    2. Path Difference
    3. Adding waves using phasors
  6. Intensity
    1. Connection to Power
    2. Connection to Sound Level (dB)
  7. Optics – Reflection
    1. Mirror types
    2. Sign convention
    3. Ray tracing
  8. Optics – Refraction
    1. Index of refraction
    2. Snell’s law
    3. Lenses
    4. Sign convention
    5. Ray Tracing
  9. Diffraction
    1. Single Slit Diffraction
    2. Double Slit Diffraction+Interference
  10. Nature of light
    1. Electromagnetic spectrum
    2. Effect of material density
    3. Effect of reflections
  11. Electricity
    1. Coulomb Force
    2. Electric Fields
    3. Electric Potential and Potential Energy
  12. Magnetism
    1. Right-Hand Rule
    2. Lorentz Forces
    3. Biot-Savart Law

UNIVERSITY MATH

Calculus 1 - Term 1A

Calculus 1 builds upon the high school equivalent. It reviews all common functions and manipulation thereof. The course works more closely with the fundamental definition of the limit and derivative and uses them to establish the meaning of continuity and differentiability for functions. It teaches the odd nature of infinitesimals and the way we use them to approximate roots to functions and function behavior overall. It ends by establishing the notion of the integral along with popular methods in handling antiderivative problems.

  1. Functions
    1. Trig/Exp/Log
    2. Transformations
    3. Compositions
    4. Inverses
    5. Odd vs Even
    6. Piecewise
    7. Heavyside
  2. Domain and Range
  3. Absolute value inequalities
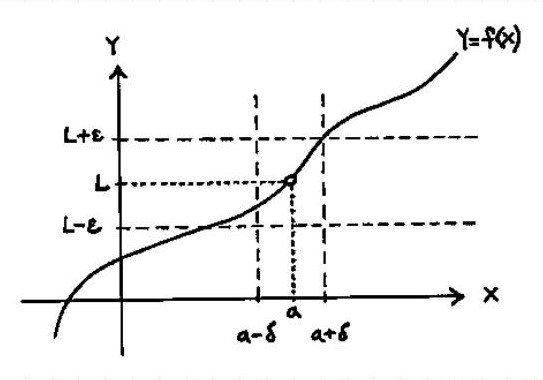
  4. Limits
    1. Definition of Limit
    2. Continuity
    3. Sequence Limits
    4. Function Limits
  5. Derivatives
    1. Definition of Derivative
    2. Common derivatives
    3. Product Rule
    4. Quotient Rule
    5. Chain Rule
    6. Implicit Differentiation
    7. Logarithmic Differentiation
  6. Derivative Applications
    1. Critical Points
    2. Concavity & Inflection Points
    3. Optimization
  7. Approximation Techniques
    1. Linearization
    2. Intermediate Value Theorem
    3. Bisection Algorithm
    4. Newton’s Method
  8. Integration 1
    1. Right/Left hand Integration
    2. Definite & Indefinite Integrals
    3. Simple Antiderivatives
    4. Fundamental Theorem of Calculus
    5. Improper Integrals
  9. Integration Techniques
    1. U-Substitution
    2. Integration by Parts
    3. Trig Substitution
    4. Trig Integrals
    5. Integration by Partial Fractions
  10. Integration Applications
    1. Areas between curves
    2. Arclength
  11. Polar Coordinates
    1. Switching to Cartesian and back
    2. Polar curves
    3. Polar areas between curves
    4. Polar arclength
  12. Complex Numbers

Calculus 2 - Term 1B

Continuing from Calculus 1, the student reviews all common integration techniques first. Applications of integration immediately follow. Students can now measure lengths of curves, areas of regions, even volumes of solids using integration. The course continues by introducing the student into the world of series. The student learns how to judge if a series is finite, and furthermore learns how to approximate complicated functions as infinite chains of polynomial powers (Power Series), the ultimate approximation tool in math!

  1.  Review of Integration
    1. Fundamental Theorem of Calculus
    2. All Techniques
    3. Improper Integrals
  2. Geometric Applications of Integration in Cartesians & Polars
    1. Arclength
    2. Area between Curves
    3. Volume of Solid of Revolution (Washer Method)
    4. Area of Solid of Revolution (Cylinder Method)
  3. Parametric Equations
    1. Common Parametrizations
    2. Parametric Derivatives
    3. Parametric Arclength
    4. Parametric Area between Curves
    5. Vector Valued Functions
  4. Numerical Integration
    1. Rectangle Rule
    2. Trapezoid Rule
    3. Simpson’s Rule
    4. Upper Error Estimates
  5. Differential Equations
    1. 1st Order, Separable
    2. 1st Order, Integrating Factor
    3. 2nd Order, Reduction by Substitution
  6. Sequences
    1. Recursive Formulae
    2. Monotone Sequence Theorem
    3. Limits
  7. Special Series
    1. Geometric Series
    2. p-series
    3. Telescoping Series
  8. Series Convergence Tests
    1. p-series Test
    2. Geometric Series Test
    3. Divergence Test
    4. Integral Test and Remainder Theorem
    5. Comparison Test
    6. Limit Comparison Test
    7. Ratio Test
    8. Root Test
  9. Alternating Series
    1. Absolute vs Conditional Convergence
    2. Alternating Series Test
    3. Alternating Series Remainder Theorem
  10. Power Series
    1. Deriving from base cases
    2. Taylor Series
    3. Taylor Remainder Theorem
    4. Radius of Convergence
    5. Interval of Convergence

Linear Algebra - Term 1A

In this course, students get introduced into complex numbers and their algebra. Vectors provide a natural follow-up and operations between them are investigated. Continuing, the course employs vectors to describe geometrical objects such as lines, planes and hyperplanes. Finding the intersections of these naturally leads to solving systems of linear equations using matrices. Further applications of matrices in probability, circuits, and flow are usually explored. Students learn how to construct a basis. Various operations such as projections, rotations and reflections are turned into linear maps, whose determinants tell us a lot about their effect on a given input. Finally the students learn about special inputs (eigenvectors) that only get scaled by linear operators and unlock impressive capabilities such as calculating matrix powers and constructing fundamental basis sets!

  1. Complex Numbers
    1. Polar Form
    2. Standard Form
    3. Addition/Subtraction
    4. Multiplication/Division
    5. Norm
    6. De Moivre’s Theorem
    7. Roots of Complex Functions
    8. Proofs
  2. Vectors
    1. Addition/Subtraction
    2. Norm
    3. Dot Product
    4. Cross Product
  3. Geometry
    1. Equations of Lines (Vector, Parametric and Standard Form)
    2. Equations of Planes (Vector, Parametric and Standard Form)
    3. Intersections
    4. Minimizing Distance
    5. Proj and Perp Operators
  4. Matrices
    1. Addition/Subtraction
    2. Multiplication
    3. Row Reduction
    4. Row Echelon Form (REF)
    5. Reduced Row Echelon Form (RREF)
    6. General Solutions (Single, Infinite, None)
    7. Column Space
    8. Row Space
    9. Null Space
    10. Trace
    11. Symmetric
    12. Upper/Lower Triangular
  5. Applications of Matrices
    1. Stochastic Matrices
    2. Adjacency Matrices
    3. Flow Diagrams
    4. Circuits
  6. Spanning Sets
    1. Linear Dependence and Independence
    2. Dimension
    3. Reduction of a Spanning Set
    4. Basis Conditions
    5. Orthogonal & Orthonormal Basis
    6. Gram-Schmidt Method
  7. Subspaces
    1. Sets (Intersection, Union, Sum)
    2. Proving a Subset is a Subspace
    3. Deriving a Subspace’s Spanning Set
    4. Polynomial Spaces
  8. Linear Maps
    1. 1-to-1 and Onto
    2. Proving a Map is Linear
    3. Deriving a Map’s Transformation Matrix
    4. Inverses
  9. Determinants
    1. 2×2 Determinants
    2. Cascade Pattern for nxn Determinants
    3. Cofactor Expansion Matrix (Cij)
    4. Adjoint Matrix
    5. Connection to Inverses
    6. Properties
  10. Eigenspaces
    1. Eigenvalues
    2. Eigenvectors
    3. Diagonalization
    4. Matrix Powers

Statistics & Probability - Term 1B

In this type of course students learn how to analyze data and organize it into sets. The course begins with analyzing phenomena with discrete outcomes, such as the roll of a fair die, and continues into exploring phenomena in a continuous population using Gaussian statistics. By the end of the course students employ their skills to construct linear models to describe correlations between dependent and independent variables in various scenarios!

  1. Set Theory
    1. Union
    2. Intersection
    3. Sum
  1. Discrete Statistics
    1. Sample Space
    2. Relative and Cumulative Frequency
    3. Histograms
    4. Stem-and-Leaf Plots
    5. Mean, STD, Variance, z-score
    6. Coefficient of Variation
  1. Discrete Probability
    1. Classical Probability
    2. Weighted Probability
    3. Joint Event Probability
    4. Conditional Probability
    5. Marginal Probability
    6. Exclusion Probability
    7. The Binomial Distribution
    8. The Bernoulli Distribution
    9. The Poisson Distribution
  1. Continuous Statistics
    1. Uniform Probability
    2. Chebyshev’s Theorem
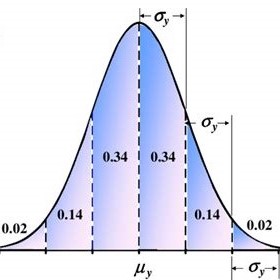
    3. The Empirical Rule
    4. Intro to the Normal Distribution
  1. Gaussian Statistics
    1. Infinite Sample Size
    2. Finite Sample Size
      1. Falling within a range
      2. Probability of a success/fail and fractions (qp stats)
  1. Single Population Hypothesis tests
    1. Left-Tail, Right-Tail, 2-Tailed
    2. Forming a test
    3. “t” vs “z” statistics (Sample vs Population)
    4. Level of significance and level of confidence
  1. 2-Independent Population Hypothesis tests
    1. Population STDs are known (z-statistics)
      1. Calculating mixed population STD
      2. Calculating Confidence Interval
      3. Calculating z-score
    2. Population STDs are unknown but equal (t-statistics)
      1. Calculating Degrees of freedom
      2. Calculating Sample STD
      3. Calculating Confidence Interval
      4. Calculating t-score
  1. Simple Linear Regression (Least Squares)
    1. Coefficient of correlation “r”
    2. Variation of “x” (SSx) and “y” (SSY) variables
    3. Covariation of “x” and “y” (SSxy)
    4. Standard error of estimate (Se)
    5. Mean Square due to regression model (MSR)
    6. Mean Square due to errors (MSE)
    7. Variation due to errors (SSE)
    8. Variation due to regression model (SSR)
    9. Confidence Interval in a y value given an x value
  1. Multi-Linear Regression
    1. Expanding all ideas for the quantities in previous section
    2. Adjusted r-squared parameter
    3. Residual analysis
    4. Types of Variables
      1. Nominal
      2. Ordinal
      3. Categorical
      4. Continuous
    5. Problems introduced by:
      1. Collinearity
      2. Non-Linearity
      3. Small Sample Size compared to Variable Number
      4. Identifying the independent/dependent variable

Calculus 3 - Term 2A

In this course students begin by expanding the idea of the derivative in the multivariable world. They learn how to find directions of maximum change using the gradient and global as well as local critical points along a scalar function. Different 3D coordinate systems are investigated and used to solve double and triple integrals pertaining to applications such as finding moments of inertia, volumes and center of mass. Each point suddenly corresponds to a direction and the Cartesian grid suddenly turns into a vector field. Sources/Sinks and the concept of rotation in a field are investigated. The distinction between integrating a vector vs scalar function is made clear and the course closes with some fundamental theorems allowing the student to opt for an easier approach to otherwise impossible integration problems.

  1. Derivatives of Multivariable Functions
    1. Partial Derivatives
    2. Chain Rule for Explicit Functions
    3. Chain Rule for Implicit Functions
  2. The Gradient
    1. Finding Max/Min rate of change
    2. Directional Derivatives
  3. Critical Points
    1. Global Critical Points
    2. Local Extrema (Lagrange Multipliers)
  4. Length, Volume and Area Elements
    1. In Cartesians
    2. In Cylindricals
    3. In Sphericals
  5. Double Integrals
    1. Constant Bounds
    2. Iterated Integrals
    3. Applying 1D Integral Methods (U-Sub, Trig Sub, etc.)
    4. Change of Order
    5. Conversion to Polars
    6. Parametrization and the Jacobian
    7. Finding the Centroid of a region
    8. Finding the Volume of Revolution
  6. Triple Integrals
    1. Intersections of Surfaces
    2. Volume of Solid
    3. Moment of Inertia
    4. Center of Mass
  7. Vector Fields
    1. Drawing Vector Fields
    2. Curl
    3. Divergence
  8. Line Integrals
    1. Common parametrizations
    2. Line Integrals of Scalar Functions
    3. Line Integrals of Vector Fields
    4. Fundamental Theorem of Line Integrals
  9. Surface Integrals
    1. Surface Integrals of Scalar Functions
    2. Surface Integrals of Vector Fields
  10. Fundamental Theorems
    1. Green’s Theorem
    2. Stoke’s Theorem
    3. The Divergence Theorem

OTHER UNIVERSITY COURSES

Introduction to Astronomy - Term 1A or 1B

This course as the name suggests prepares students for the physics behind the cosmos! The typical course here begins by visiting ancient astronomy and its progression through time. Students then "zoom out" from astronomy governing the Earth, the Solar System, out Milky Way galaxy and progressively make their way to the entirety of our observable universe, but with no significant mathematical analysis as this is preserved for higher-year astronomy courses.

  1. Astronomy with the Human Eye

    1. The Local Sky

    2. Moon Phenomena

    3. Measuring Time

    4. Measuring Distance

    5. Celestial Coordinates

  2. Astronomy through time

    1. Heliocentrism vs Geocentrism

    2. Telescope evolution

    3. Major astronomical discoveries

  3. The Earth & Moon System

    1. Formation of Earth & Evolution

    2. Earth’s atmospheric layers

    3. Earth’s Magnetic Field & Aurorae

    4. The Greenhouse effect

    5. Tectonic Plates & Volcanism

    6. Asteroid Impacts

    7. The Milankovich Cycles

    8. Moon formation

    9. Moon atmosphere & surface

    10. Tides

  4. The Solar System

    1. The Nebular Hypothesis

    2. Condensation Theory

    3. The 7 planets

    4. Radio Reflection for Distances (Distance Ladder 1)

    5. Noteworthy Moons

    6. Dwarf planets

    7. Asteroids, comets, meteors

    8. The Asteroid Belt and Oort Cloud

    9. The Sun

    10. Kepler’s Laws

    11. Newton’s Law of Gravitation

  5. Light & Matter

    1. E&M Spectrum

    2. Refraction, Diffraction, Interference

    3. Speed of light in different media

    4. Blackbody Radiation

    5. The Photoelectric Effect

    6. Compton Scattering

    7. Emission/Absorption Spectra

    8. The Bohr Atom

  1. Exoplanet Methods

    1. Direct Observation

    2. Radial Velocity Method

    3. Transit Method

    4. Gravitational Lensing Method

  1. Normal Stars

    1. Parallax for Distances/Sizes (Distance Ladder 2)

    2. Proper Motion

    3. The Magnitude system

    4. The concept of Color

    5. Spectometry

    6. The Spectral and Luminosity Classes

    7. Intensity and Stephan Boltzmann’s Law

    8. The Hertzsprung-Russel Diagram

    9. Luminosity-Mass Power laws

    10. Star Formation Theory leading up to Main Sequence

    11. The Giant Branch

    12. The Supergiant Branch

    13. Globular vs Open Clusters

  1. Degenerate Stars

    1. Shell Burning

    2. Electron Degeneracy & Novae

    3. White Dwarfs

    4. Type Ia & Ib Supernova (Feeding White Dwarf)

    5. Type II Supernova (Supergiant Collapse)

    6. Black Holes & Hawking Radiation

    7. Neutron Stars & Pulsars

    8. Quark Stars

    9. Gamma Ray Bursts

  1. The ISM

    1. Emission, Reflection and Dark Nebulae

    2. HII Regions

    3. The Messier Catalogue

    4. 21cm Emission

  1. The Milky Way

    1. Type, Size, Shape, Mass

    2. The Spiral Arm mechanics

    3. RR Lyrae & Cepheid Variable Stars (Distance Ladder 3)

    4. The Central Bulge & Supermassive Black Hole

    5. The Dark Matter Halo & Rotation Curve Anomaly

    6. Galaxy Formation Theory

  1. Local Group

    1. Member Galaxies

    2. Spirals, Elliptical, Lenticular and Irregular Classes

    3. Proper motion of stars in other Galaxies

    4. Rotation Curves for Distance (Distance Ladder 4)

    5. Supernovae for Distance (Distance Ladder 5)

  1. Large Scale Structure

    1. The Virgo Cluster

    2. Hubble’s Law & Redshift (Distance Ladder 6)

    3. The Hubble Constant

    4. Dark Matter seeding Galaxy Formation

    5. Calculating the Mass of a Galaxy Cluster

    6. Collisions of Galaxies

    7. The Virgo Supercluster

    8. The Great Wall

    9. Olber’s Paradox

  1. The Expanding Universe

    1. Hubble Flow

    2. Universe Geometries (Flat, Closed, Open)

    3. The Friedman Equation

    4. Critical Density and The Omega Parameters

    5. Universe Fates (Big Crunch, Big Rip)

    6. Strong and Weak Equivalence Principles

    7. The Einstein Field Equations (Only Discussing)

    8. The Cosmic Microwave Background

    9. Inflation

    10. The Drake Equation

1st Year Labs - Term 1A and 1B

These labs are usually complimentary to the Classical Mechanics course mentioned above. They conduct various table-based experiments aimed at proving or carrying out concepts that were taught in-class. They also teach the student how to carry proper uncertainty analysis, significant digits and formal report-writing etiquette.

1) Report Writing

2) Hypothesis Formulation

3) Calculating Uncertainties

4) Equation Derivations

5) Data Analysis and Regression

6) Coding

7) Explanation and advice on an upcoming experiment

8) Report Editing